Multiplication Table for Elementary Students: Detailed Guide

Mastering the multiplication table is essential for building math fluency, problem-solving skills, and confidence in students. Here's what you need to know:

• What a multiplication table is: A grid that organizes products of number pairs, showing patterns and relationships.

• Why it's useful: Knowing multiplication facts is the most useful way to make division. Also, it speeds up calculations, supports advanced math (like fractions and algebra), and is practical for everyday tasks like budgeting or time management.

• When kids learn it: Typically introduced in 2nd grade and learned in 3rd grade (ages 8-9), but readiness depends on understanding addition, skip counting, and grouping.

• A self-made table is a must-do, and not once.

• Memorization vs reasoning: Combining understanding with quick recall ensures both speed and flexibility in solving problems.

• Fluency-building tips: Use skip counting, visual aids, games, and short practice sessions. Finger tricks and patterns (like for the 9s) can make learning engaging.

• Challenges for special learners: For children with ADHD or dyscalculia, multisensory tools, smaller steps, and personalized strategies work best.

Takeaway: If multiplication tables are more than just memorization, but reasoning also, they're a foundation for math success. Use a mix of methods to make learning effective and enjoyable.

What is a Multiplication Table?

A multiplication table is an arranged grid that displays the products of number pairs. Picture it as a chart where each box shows the result of multiplying the number from its row by the number from its column. This layout simplifies understanding multiplication by highlighting patterns, relationships, and the structured nature of numbers.

But it’s not just a quick-reference tool. A multiplication table offers a visual snapshot of how numbers interact, helping students grasp the logic behind multiplication.

What Multiplication is

Multiplication is most clearly represented as the area of a rectangle. For example, 4 × 3 can be shown as 4 rows of 3 squares. This way of defining multiplication helps children avoid getting stuck on the order of the factors. On the contrary, it immediately makes commutativity clear: a 3×4 rectangle, a 4×3 rectangle, and a 2×6 rectangle contain the same number of squares.

After that, we can move on to the definition based on repeated addition. For example, when we calculate 4 × 3, we’re adding 4 three times: 4 + 4 + 4 = 12.

This idea of repeated addition is often visualized through grouping — for instance, 3 groups of 4. Then we get an interesting fact:

4 + 4 + 4 = 3 + 3 + 3 + 3

It’s a real meaning of the commutativity law, and you may ask children to write 70 as the sum of 10s or a sum of 7s, for example:

10 + 10 + 10 + 10 + 10 + 10 + 10 = 7 + 7 + ________

Multiplication has other properties as well. Identity (any number multiplied by 1 stays the same) can be illustrated with the area of a rectangle that has one side equal to 1.

Associativity – for example, that ((3 × 3) × 2 = 3 × (3 × 2)) can be shown in the same way - just making a brick of 3 × 3 × 3 cubes.

The zero property (any number multiplied by 0 equals 0) is the most complex one, as it comes down to convenience and convention. All these properties make calculations more intuitive and manageable.

What a Table is (Mathematical Context)

In math, a table is a grid of rows and columns used to organize data. This format makes information easy to read and navigate, allowing users to quickly locate specific details. Make sure that before beginning work with the multiplication table, children can easily handle filling in simple tables like this one:

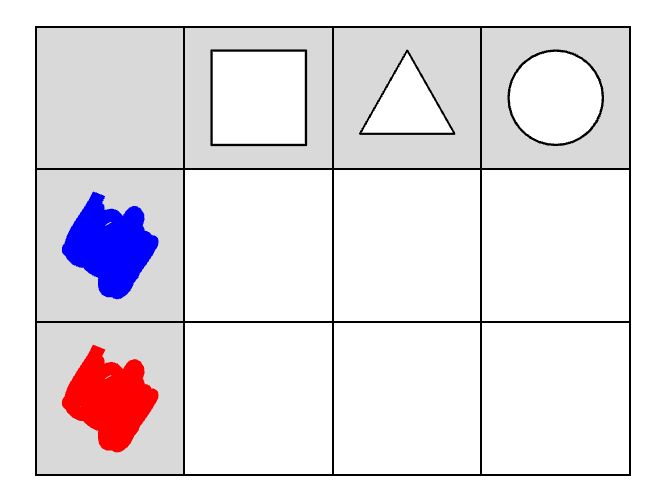
This problem is more like the multiplication table.

A standard multiplication table typically includes numbers 1 through 12 along the top row and the leftmost column. Each cell in the grid represents the product of the intersecting row and column numbers. For instance, where row 6 meets column 7, you’ll find 42, because 6 × 7 = 42.

This grid structure also uncovers key mathematical patterns. For example, it’s easy to spot that multiplying any number by 2 always results in an even number, or that products involving 5 always end in 0 or 5. These patterns make the table a powerful tool for learning and memorization.

Additionally, the table’s systematic design encourages logical thinking. Students quickly learn to navigate the grid, recognizing that answers are mirrored thanks to the commutative property of multiplication (e.g., 6 × 7 is the same as 7 × 6). This not only reinforces their understanding of multiplication but also builds problem-solving skills.

Understanding multiplication as repeated addition lays the groundwork for more complex math. It bridges naturally to division (its inverse operation), fractions (parts of groups), and even algebra (where variables represent numbers in multiplication problems). That’s why schools emphasize learning multiplication tables - they’re a cornerstone for building strong math skills and fluency.

Preparing to learn the multiplication table

My multiplication table

When children understand how the table is organized, it’s the perfect time to make their own!

The first filling-in can be done as a group activity. The teacher prepares and prints cards for all the cells of the table. Children take the cards one by one, draw the corresponding rectangle, count the squares, and write the answer into the correct cell of the table. Parents can do the same activity over the summer, completing just a few examples each day.

Once the table is ready, it’s important to discuss its properties.

• How is the commutative property reflected in the table — the fact that 4×6 and 6×4 give the same answer?

• Where in the table do we find the numbers ending in 0?

• Where do we find the even numbers?

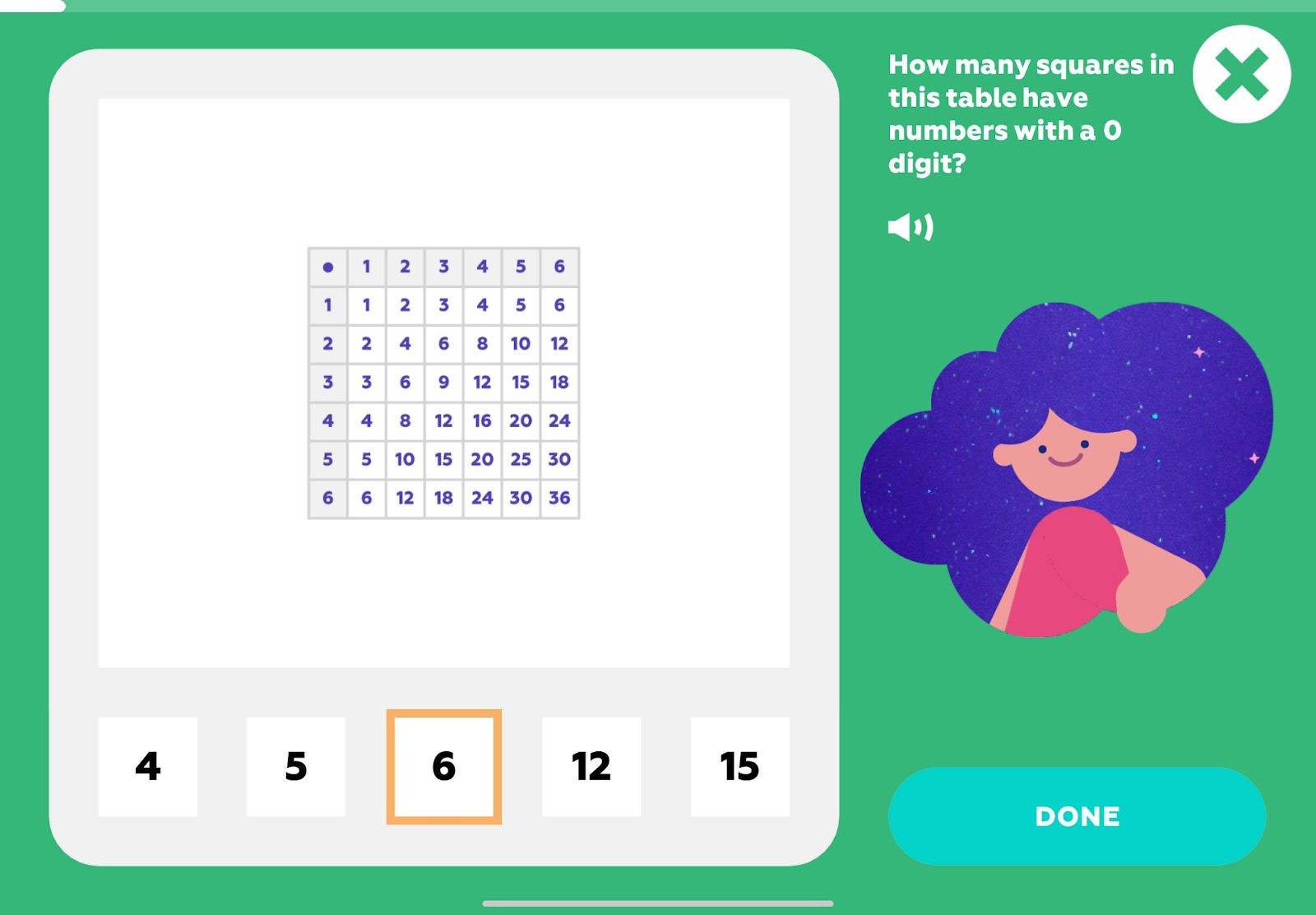
• How many times does the number 24 appear in the table? What about 9?

• Which numbers appear an odd number of times?

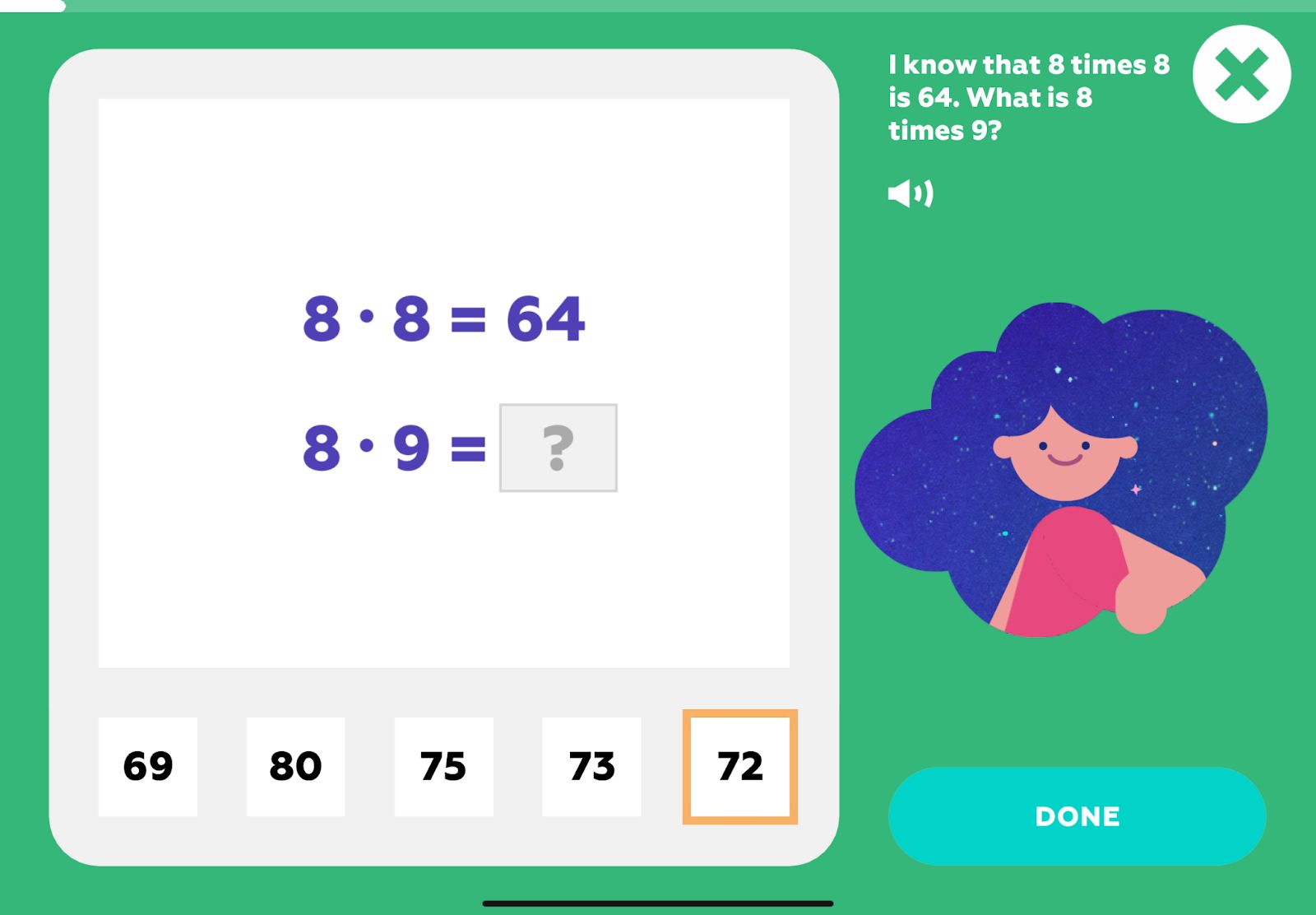
You can cover one of the cells and ask how to find this product by using the neighboring products. Children can, for example, figure out how to find 8×9 if they know 8×8. This kind of work is essential for understanding.

After such a thorough exploration, you can give children an empty table and ask them to fill it row by row. Skills such as addition and skip counting will help. Offer the same task again a week or two later — you’ll see that each time they complete it significantly faster.

It makes sense to start by filling in the columns you already know — multiplication by 1, 10, 2, and 5 — and then complete them with facts that have already been learned, such as the squares of numbers. The multiplication table for 4 can be filled in halfway by looking at the table for 2: you simply take every other number. And so on.

As children progress, the table does not need to be filled in all at once. You can focus on just part of the numbers — for example, multiplying only 3, 6, and 9 by 2 and 5.

The same kind of tables can later be used for multiplying multi-digit numbers. For example, the product 25 × 369 is the sum of all the partial products in such a table:

Which Numbers are in the Multiplication Table

The standard multiplication table taught in the US schools is carefully structured to align with children's developmental stages, progressing through the elementary grades. This systematic approach helps parents and educators set realistic expectations for how and when kids will grasp multiplication concepts.

In the early years - 1st and 2nd grades - students begin with skip counting by 2s, 5s, and 10s[1]. This foundational skill is a stepping stone to understanding multiplication, as it introduces patterns and sequences that make learning multiplication facts easier later on.

By 3rd grade, multiplication becomes a core focus. According to the Common Core State Standards for Math (3.OA.7), students are expected to "fluently multiply and divide within 100" and "know from memory all products of two one-digit numbers" by the end of the year[2]. In practical terms, this means mastering the 1-9 multiplication table, covering facts like 7×8=56 and 9×9=81. Many schools also include the 10 times tables at this stage[3]. The scope broadens in 4th grade, where students are required to memorize the 1-12 multiplication table (up to 12×12)[1]. This expanded range forms the core of elementary math education, as it equips students with the tools they’ll frequently use in real-life situations.

Why stop at 12? The 1-12 range is practical and widely applicable. From counting dozens to working with feet and inches, these numbers pop up often in everyday scenarios[4][5][6]. Memorizing the full 12×12 table involves 144 facts[7], a challenging but achievable goal for most elementary students.

For those who excel, some schools introduce extended tables, such as multiplication up to 20 or even using 1-100 charts to explore more complex calculations[7][5]. These advanced exercises are particularly helpful in upper elementary grades, where students begin working with larger numbers and more intricate math problems[1].

Teachers often highlight patterns and tricks to make learning easier. The 2s, 5s, and 10s tables build on familiar skip-counting rhythms, while the 9s table features unique finger tricks and predictable patterns. Even the trickier 7s and 8s become less daunting when students connect them to facts they already know.

Why Knowing Multiplication Matters Today

What about calculators? In the 19th and even the 20th century, fast mental calculation was essential. Children today may argue that with calculators around, knowing the multiplication table is no longer important. This is a meaningful argument we need to address; otherwise, children may lose motivation. One way to do this is to set up a small competition: choose a child who already knows part of the table and another who will compute the same examples on a calculator. In practice, recalling the answer is often faster than typing the expression into the calculator.

Division and factoring numbers. Knowing the multiplication table is especially important when performing division. How do we solve 56 ÷ 7? Dividing 56 objects into 7 groups would take far too long; in reality, we look for the number that multiplied by 7 gives 56 — that is, we recall the multiplication table. For this reason, children must know the examples not only in order (3×1, 3×2, 3×3, and so on) but also in mixed form: which examples give 56? What about 48? The same questions appear when factoring numbers, a skill that becomes essential when working with fractions.

Multiplication fluency is the cornerstone of math education, forming the base for nearly every mathematical concept students encounter. Without a solid grasp of basic multiplication facts, students often struggle with division, fractions, decimals, percentages, and even algebra. For example, pausing to calculate 7×8 not only slows down problem-solving but also diverts mental energy away from more complex reasoning. This skill isn’t just for academics - it plays a vital role in everyday problem-solving too.

Practical uses of multiplication are everywhere. Whether it’s calculating the total cost of groceries, figuring out travel times, or deciding how many pizzas to order for a party, multiplication is an essential tool. These real-life scenarios show students that math isn’t just a classroom exercise - it’s a skill they’ll use throughout their lives.

Mastering multiplication also strengthens overall mental math abilities. It boosts number sense, helps with recognizing patterns, and sharpens logical thinking. These skills carry over into other areas, like science, where a student might need to calculate the total legs on six spiders or analyze data. Multiplication fluency builds a foundation for tackling quantitative challenges across subjects.

Even in a technology-driven world, multiplication remains essential. Sure, calculators are handy, but students need to estimate results quickly to ensure their answers make sense. Plus, there are times when technology is unavailable. Whether it’s solving problems on the fly or preparing for STEM careers, having a strong grasp of multiplication builds confidence and competence. Professions such as engineering, architecture, programming, and data analysis rely heavily on this foundational skill.

Academic success is tied to multiplication mastery. Students who struggle to learn their times tables in third grade often face challenges with fourth-grade concepts like long division. This gap can grow wider over time, making it harder for students to catch up without extra support. Quick recall of multiplication facts not only helps with math performance but also reduces anxiety. A student who instantly knows that 6×9 equals 54 feels more capable when facing word problems, multi-step equations, or standardized tests. This confidence encourages them to tackle harder problems and stick with them.

Multiplication also unlocks advanced mathematical concepts. Students who know their multiplication tables can more easily grasp square roots, exponents, algebraic factoring, and geometry. These skills are essential for high school math, college STEM courses, and many career paths. Mastering multiplication early sets the stage for lifelong opportunities in education and beyond.

When Children Are Ready to Learn Multiplication

Figuring out when a child is ready to tackle multiplication can make all the difference between a smooth learning journey and a frustrating experience. In the U.S., schools typically introduce the basics of multiplication in 2nd grade (around age 7) to learn it intensively in 3rd grade (around age 8). However, readiness is less about age and more about a child's understanding of basic math concepts [8][9]. This timing helps ensure that children can build on these skills as they move through elementary school.

The foundation for multiplication starts in second grade, when kids begin exploring concepts like skip counting and understanding how multiplication connects to addition. These early lessons set the stage for mastering multiplication later on.

A strong grasp of addition and subtraction is critical. Without being comfortable with simple sums, solving problems like 3×8 can feel overwhelming [10]. Mental addition skills, such as adding one-digit numbers to two-digit numbers, also play a big role in developing the stepping-stone skills needed for multiplication [10].

Beyond basic skills, understanding the concept of multiplication is just as important. For example, knowing that "3×8" means "three groups of eight" helps children see multiplication as more than just a math problem [10]. Kids should be familiar with the idea of equal groups and understand that multiplication is a form of repeated addition [11][12].

Skip counting is another sign that a child is ready. When kids can confidently count by 2s, 5s, and 10s - skills often introduced as early as kindergarten - they develop the pattern recognition needed to tackle multiplication tables [11][13]. This also naturally leads to understanding key math properties, like the commutative property, which simplifies multiplication. For example, knowing that 4×6 is the same as 6×4 shows flexible thinking that makes learning easier [12].

It’s important to remember that these grade levels are meant to be guidelines, not hard rules. Every child learns at their own pace. Some kids, like those in gifted programs, might start learning multiplication earlier, while others may need more time to develop the necessary skills [8][9].

For children who face challenges with processing or memory, such as those with learning differences, extra time to strengthen foundational skills can make a huge difference [10][14]. Rather than pushing a child who isn’t ready, focusing on building up their confidence with addition, subtraction, and mental math can set them up for success later on.

Parents and teachers can play a big role in supporting readiness. Reinforcing early addition skills and encouraging mental math can help kids feel more confident. Starting with simple patterns, like the 2s, 5s, and 10s multiplication tables, allows children to experience early wins, boosting their confidence for tackling harder problems.

Learning the multiplication table

Memorization vs. Understanding: Finding the Right Balance

The long-standing debate in U.S. classrooms - whether to focus on memorizing multiplication facts or understanding the concepts behind them - has no simple answer. Both approaches play an important role, and the best learning happens when kids develop automatic recall alongside deep conceptual understanding.

Memorization builds speed and confidence. When students can instantly recall that 7×8=56, they free up mental energy for tackling more challenging problems. This fluency becomes critical in fourth and fifth grades, where multi-digit multiplication, fractions, and word problems come into play. Without quick recall of basic facts, students often get bogged down in calculations, losing sight of the bigger mathematical ideas they need to grasp.

That said, memorization alone has its limits. Students who rely solely on rote memory may struggle when they forget a fact or face an unfamiliar problem. For example, they might know 6×7=42 but feel stuck if they can't recall it. This is where conceptual understanding steps in.

Understanding gives students flexibility and problem-solving power. When kids truly understand that multiplication represents "groups of" or "repeated addition", they can approach problems in multiple ways. For instance, a student who forgets 6×7 might think, "I know 6×5=30 and 6×2=12, so 6×7 must be 30+12=42." This kind of flexible thinking becomes an invaluable tool throughout their math journey.

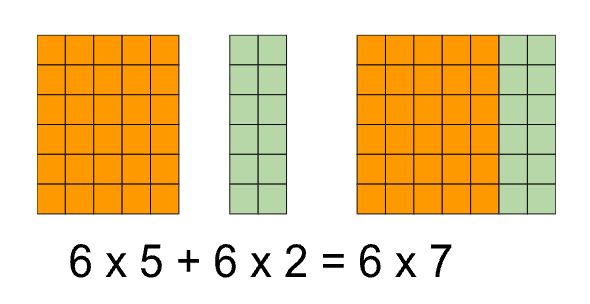
The most effective learning combines both memorization and understanding. Research consistently shows that students thrive when they grasp multiplication concepts and can recall facts quickly. Teachers can achieve this by starting with conceptual understanding and then building fluency.

Start with understanding, then build fluency. Many effective teachers begin by helping students visualize multiplication using arrays, groups, and real-world examples. For instance, showing that 4×3 means "four groups of three objects" lays the groundwork for memorizing that 4×3=12.

Use understanding to make memorization meaningful. Instead of drilling random facts, help kids notice patterns and connections. For example, the 9s table has a clever finger trick based on mathematical patterns, while the 2s, 5s, and 10s tables connect to skip counting and money. Recognizing these patterns makes memorization easier and more engaging.

Make memorization active, not passive. Rather than having kids repeat facts mechanically, encourage them to explain their thinking, explore multiple strategies, and find connections. For example, a student working on 8×6 might calculate it as 8×5+8×1, double 4×6, or apply the commutative property (6×8 instead of 8×6).

This balanced approach works well for children with different learning styles. Visual learners might benefit from arrays and pictures, while auditory learners may prefer songs and chants. Kinesthetic learners often thrive with hands-on activities and movement-based games.

Timing matters too. Pushing memorization too early - before kids understand the underlying concepts - can lead to math anxiety. On the flip side, focusing only on understanding without developing fluency can leave students struggling with speed and confidence later on. The key is to meet children where they are in their learning journey and provide the right support at the right time.

To nurture both recall and reasoning, teachers and parents can ask thoughtful questions that encourage deeper thinking. Instead of just asking, "What's 7×4?" try, "What's 7×4, and how do you know?" or "Can you think of another way to solve 7×4?" These types of questions promote both quick recall and flexible problem-solving.

How to Build Multiplication Fluency

Helping children develop multiplication fluency takes consistent and effective practice. When kids can quickly and accurately recall multiplication facts, they free up mental energy for tackling more complex math problems.

According to NCTM and the Common Core Standards, fluency is not just speed or memorization. It consists of three components:

• Accuracy — answering correctly;

• Efficiency — using strategies that minimize unnecessary effort

• Flexibility — choosing and shifting between strategies as needed.

Modern research in math cognition shows that children who develop all three components perform better not only in arithmetic but also in multi-step problem solving, fractions, and algebra. Fluency supports working memory: when multiplication facts are retrieved automatically, the brain can focus on reasoning (Geary, 2013; Fuchs et al., 2014)[15][16].

At the same time, research consistently shows that simple rote memorization without strategies is ineffective for long-term learning. Children may recall facts on a quiz but forget them weeks later, or fail to apply them flexibly in new contexts. Strategy-based practice — arrays, decomposition, doubling-and-halving, using known facts — leads to deeper, more durable understanding (Baroody, 2006; Siegler & Lortie-Forgues, 2015)[17][18].

Here are some practical, research-aligned strategies to build fluency step by step:

Start with skip counting to recognize patterns. Skip counting is a great way to introduce multiplication. Begin with easy patterns like counting by 2s, 5s, and 10s since these are often encountered in daily life. Once children are comfortable, move on to counting by 3s, 4s, and other numbers. This approach helps kids see how numbers grow and builds a foundation for multiplication.

Group facts into families to simplify learning. Teaching multiplication in related groups, or "fact families", makes it easier for children to spot connections. For example, understanding the relationship between the 2s, 4s, and 8s tables - like how doubling a number leads to the next fact - reduces the number of facts they need to memorize and deepens their understanding of multiplication.

Use visual tools and hands-on activities. Visual aids like arrays (e.g., arranging 12 objects into 4 rows of 3) help children see how multiplication works. Using manipulatives like blocks, beans, or cereal pieces can make learning more interactive and reinforce the concept of grouping numbers. These tools also highlight the commutative property of multiplication - how 3 × 4 is the same as 4 × 3.

Keep practice sessions short and frequent. Instead of long, exhausting study sessions, aim for short bursts of practice. Spending 10–15 minutes a few times a week is much more effective and helps transfer knowledge from short-term to long-term memory without overwhelming the child.

Add movement and rhythm for better retention. Many kids learn more effectively when movement or rhythm is involved. Try clapping while reciting multiplication facts, using jump ropes to practice skip counting, or singing multiplication songs. These activities create memorable patterns and make learning more engaging.

Turn practice into a game. Learning is more fun when it feels like play. Use interactive tools like Funexpected Math, which offers games and activities tailored to a child's learning pace (all the visuals in this article are taken from the Funexpected Math app). Quality platforms make practice enjoyable while helping kids grasp concepts faster. Plus, they allow parents and teachers to track progress and address mistakes early.

Start simple to build confidence. Begin with easier facts like the 1s, 2s, 5s, and 10s tables. Mastering these early on gives children a sense of achievement and the confidence to tackle harder facts later. Once they feel secure with the basics, gradually introduce the other multiplication tables.

Show how multiplication applies to everyday life. Bring multiplication into real-world situations to make it feel relevant. For instance, when setting the table, you might ask, "If we need 4 plates for each of 6 people, how many plates do we need?" Or at the grocery store, explore questions like, "If each pack has 8 crackers and we buy 3 packs, how many crackers do we have?" These practical examples make multiplication more meaningful.

Spaced repetition: Spaced repetition is a learning technique where material is reviewed at progressively longer intervals to strengthen memory and improve retention over time [19]. Instead of cramming information all at once, students revisit math concepts periodically. For example, after learning addition, a child might review it the next day, then three days later, then a week later. Each successful recall allows for the interval to grow longer before the next review You can learn more about spaced repetition in this article.

Be patient and celebrate small wins. Fluency doesn’t happen overnight - it’s a process that takes months. Some facts may come easily, while others take more time. Celebrate each milestone, no matter how small, and keep practice consistent and enjoyable.

What to Avoid When Learning Multiplication Tables

Avoid starting by memorizing the entire table from 1×1 to 10×10 in strict order. Trying to learn everything at once can overwhelm a child and make the process feel like a chore.

Avoid relying solely on mnemonic tricks or gimmicks. While fun tricks or rhymes may help with a few facts, they don’t build deep understanding — and understanding is important for long-term success.

Avoid forcing memorization when the basic concept isn’t clear. If a child doesn’t yet understand what multiplication means (for example, “groups of”), then rote learning turns into a mechanical exercise without meaning.

Avoid pressuring for speed or punishing slow answers. When a child answers slowly, it often means they are thinking and reasoning — that’s good. Speed will come later; for now, understanding matters more.

Multiplication Tricks Using Fingers

Finger techniques are a fun and interactive way to build multiplication skills, offering a hands-on alternative that makes learning math more engaging. By using their fingers as tools, children can better understand numerical patterns and recall facts faster. These methods are particularly helpful for kids who learn best through physical activities, complementing other strategies like visual aids and hands-on exercises.

One of the most well-known examples is the 9s trick, a simple yet effective method for solving multiplication problems from 9 × 1 through 9 × 10. What makes this trick so helpful is how it highlights patterns in the 9 times table - like the fact that the digits in each product always add up to 9.

Here’s a step-by-step guide to teaching the 9s trick:

1. Have your child hold both hands in front of them, palms facing out, with all ten fingers spread apart.

2. Assign numbers to the fingers, starting with the pinkie on the left hand as "1" and ending with the pinkie on the right hand as "10."

3. To solve a problem like 9 × 4, locate the multiplier (4 in this case) and fold down the corresponding finger - the fourth finger from the left.

4. Count the fingers to the left of the folded finger for the tens digit, and the fingers to the right for the ones digit. For 9 × 4, there are 3 fingers on the left and 6 on the right, giving you the answer: 36.

"That said, when teaching children these tricks, encourage them to ask why these techniques work and the mathematical reasoning behind them." - Whizz Education [13]

Beyond the 9s trick, there's another method for multiplying larger numbers between 6 and 10, called the Factor-5 method. This approach builds on basic facts like 5 × 5 and simplifies calculations for numbers above 5.

Here’s how it works:

• Subtract 5 from each factor and raise that many fingers on each hand. For example, to calculate 7 × 8, raise 2 fingers on one hand (because 7 - 5 = 2) and 3 fingers on the other (because 8 - 5 = 3).

• Add the raised fingers to get the tens digit: 2 + 3 = 5 (representing 50).

• Multiply the number of closed fingers on each hand: 3 × 2 = 6.

• Add the two results together: 50 + 6 = 56.

These techniques not only make multiplication less intimidating but also give kids alternative strategies to rely on if they forget a fact. However, it’s essential to focus on understanding the logic behind these tricks rather than just memorizing the steps. A solid grasp of the reasoning helps children apply the concepts more broadly and strengthens their overall math skills.

Games for Practicing Multiplication

Turning multiplication practice into play is a great way to keep kids engaged while strengthening their math skills. By mixing different types of activities, parents and teachers can ensure kids stay motivated while keeping an eye on their progress and addressing any errors early on.

Card games are a simple, hands-on way to practice without needing technology. A popular choice is Multiplication War. In this game, two players draw cards and race to shout out the correct product of the numbers. The fastest player to answer correctly wins the round and takes the cards. This competitive element encourages quick thinking and sharpens recall in an enjoyable way.

For kids who love art, the Waldorf Multiplication Flower combines creativity with learning. Here’s how it works: children draw a flower with a number (between 2 and 12) at the center. Around it, they add 12 inner petals numbered 1–12, then fill 12 outer petals with the products of the center number multiplied by each inner petal number. This artistic approach not only reinforces multiplication patterns but also results in a colorful piece of artwork that they can proudly display.

Digital games bring an interactive twist to multiplication practice. Platforms like Funexpected Math offer interactive activities guided by a digital tutor. These games adapt to the child’s learning pace, providing a personalized experience that complements traditional hands-on and group activities.

Board games make math practice a family affair. Games like KS2 Mathopoly Times Tables and Division Facts Game combine fun and learning with elements like boards, challenge cards, and score sheets. They present multiplication (and sometimes division) in different formats, turning practice into a social activity that everyone can enjoy together.

For kids who thrive on movement, active games like times table races or ball-bouncing recitations are a great fit. These physical activities engage kinesthetic learners, making memorization part of playtime.

Calculator games are another engaging option. For example, the "Calculator Constants" method allows kids to explore number patterns visually. They select a factor (like 7), enter it into the calculator, press the "+" button, and repeatedly hit "=" to see the sequence of multiples (7, 14, 21, 28, etc.). This approach shows how multiplication connects to repeated addition.

Mixing different types of games throughout the week can make practice more effective. Starting with easier facts - like multiplying by 0, 1, 2, 5, and 10 - helps build confidence, especially since these numbers often follow predictable patterns. Gradually introducing harder facts ensures steady progress. Play during car rides, before dinner, or while waiting for appointments to turn idle time into productive learning moments. Keeping sessions brief and positive prevents stress and shifts the focus to improvement rather than perfection.

Online platforms designed for the Multiplication Tables Check (MTC) are another excellent resource. These adaptive games help students prepare for standardized tests, offering extra practice on tricky facts while quickly moving through concepts they’ve already mastered.

Helping Children with Learning Differences

Children with learning differences often face unique challenges when learning multiplication tables. Understanding these challenges is essential to finding effective ways to help. Kids with ADHD, dyscalculia, or other learning disabilities may struggle because traditional teaching methods don’t align with their cognitive needs.

One major obstacle is working memory limitations. When too much mental energy is spent on simple calculations, there’s little capacity left for grasping more advanced concepts like division or fractions. This creates a ripple effect - gaps in foundational knowledge make it harder to understand more complex topics later on.

Another common issue is the abstract nature of multiplication facts. Rote memorization, a go-to method for many, often falls short for these learners. They need to experience math in a more tangible way to truly understand it.

Timed tests and drills can also be counterproductive. For children who are sensitive to time pressure, these activities can trigger anxiety rather than improve performance. Kids with processing challenges, like those with dyscalculia, might make errors that seem careless but actually stem from genuine difficulties. This can lead to math anxiety, where stress and fear of failure create a cycle that makes learning even harder.

Thankfully, there are strategies that can make a big difference. Multisensory approaches are one such solution. By engaging multiple senses, these methods help information stick. For instance, kids can type out math facts in fun fonts, trace numbers in sand, or use physical objects like blocks to explore concepts. These hands-on activities create different ways to absorb and recall information.

Visual aids and concrete examples are also incredibly helpful. Take dot arrays, for example: a 4 × 3 array shows four groups of three dots, making the concept of multiplication more understandable and less abstract. This visual clarity helps children form meaningful connections with the material.

Breaking multiplication into smaller, manageable chunks can prevent kids from feeling overwhelmed. Instead of tackling all the tables at once, focusing on one sequence of multiples at a time builds confidence and lays a solid foundation for learning more complex facts.

Teaching students to use known facts as stepping stones is another effective technique. For example, if a child knows 5 × 6 = 30, they can use that fact to figure out 6 × 6 by adding one more group of 6. This method reduces the number of facts they need to memorize from scratch. Mnemonic programs can also help.

Pattern recognition is another powerful tool. Teaching kids to spot patterns in multiplication facts - like how multiples of 5 always end in 0 or 5, or how multiples of 2 are always even - gives them logical frameworks to lean on, reducing their reliance on pure memorization.

Digital tools can complement these strategies by offering personalized learning experiences. Platforms like Funexpected Math adapt to each child’s pace and needs, providing extra support where necessary while skipping over concepts they’ve already mastered. These tools often include multisensory activities that engage visual, auditory, and kinesthetic learners. Children can manipulate virtual objects, hear patterns, and see relationships between numbers unfold on screen, creating multiple ways to understand and retain concepts.

FAQs

How can parents tell if their child is ready to learn multiplication, and how can they help them get started?

Parents can determine if their child is ready to tackle multiplication by observing whether they have a strong understanding of addition and can count in sequences, such as by 2s, 5s, or 10s. These abilities lay the groundwork for grasping multiplication.

To ease their child into multiplication, parents might start with straightforward patterns like the 2, 5, and 10 times tables, as these are simpler to identify and remember. Incorporating real-life examples - like grouping toys or counting everyday items - can make the process more interactive and relatable.

What are some effective ways to teach multiplication to children with learning differences like ADHD or dyscalculia?

Teaching multiplication to children with learning differences calls for patience and a touch of creativity. Start by breaking the concept into smaller, easy-to-digest pieces. Using visual aids like charts, drawings, or diagrams can make abstract ideas more tangible. Hands-on tools, such as blocks or counters, are also fantastic for helping kids grasp the mechanics of multiplication in a more interactive way.

To keep things engaging, mix in fun activities like games, songs, or even movement-based exercises. These not only hold their attention but also make learning feel less like a chore. Encourage them to identify patterns in multiplication tables - like the repeated addition in the 5s or 10s - and introduce mnemonic devices to help with memorization. If a child needs more time, slow down the pace and offer plenty of opportunities for practice, which can help build both confidence and fluency.

Above all, tailor your teaching approach to suit each child’s unique needs. Celebrate every bit of progress, no matter how small - it’s a powerful way to keep them motivated and foster a positive attitude toward learning.

How can games and interactive activities help children master multiplication?

Making multiplication fun and interactive can transform how children learn. Games and hands-on activities turn what might feel like an abstract concept into something lively and engaging. This approach not only keeps kids motivated but also encourages them to practice more, which naturally leads to better understanding and memory.

Interactive tools let kids tackle multiplication at their own speed, helping them grow both their confidence and their skills. Whether they’re solving playful challenges, tackling creative problems, or enjoying some friendly competition, these activities make learning multiplication feel more like an exciting adventure than a tedious task.

Related Blog Posts

• Math Learning Milestones: Ages 3 to 7 Explained

• Early Math Skills: A Parent's Guide to Ages 3-7

• How to Teach Kids Numbers: Skills and Milestones

• How to Teach Addition in Kindergarten